- Mama
- Mama thank you for who I am
- Thank you for all the things I'm not
- Forgive me for the words unsaid
- For the times
- I forgot
- Mama remember all my life
- You showed me love,you sacrificed
- Think of those young and early days
- How I've changed
- Along the way (along the way)
- And I know you believed
- And I know you had dreams
- And I'm sorry it took all this time to see
- That I am where I am because of your truth
- And I miss you , I miss you
- Mama forgive the times you cried
- Forgive me for not making right
- All of the storms I may have caused
- And I've been wrong
- Dry your eyes (dry your eyes)
- Mama I hope this makes you smile
- I hope you're happy with my life
- At peace with every choice I made
- How I've changed
- Along the way
- And I know you believed in all of my dreams
- And I owe it all to you mama
Hederdias
quarta-feira, 23 de setembro de 2015
Mama - Il divo - lirics
quarta-feira, 15 de abril de 2015
The fourth, fifth and sixth days of God's Creation
And God said, Let there be lights in the firmament of the heaven to divide the day from the night; and let them be for signs, and for seasons, and for days, and years: And let them be for lights in the firmament of the heaven to give light upon the earth: and it was so. And God made two great lights; the greater light to rule the day, and the lesser light to rule the night: he made the stars also. And God set them in the firmament of the heaven to give light upon the earth, And to rule over the day and over the night, and to divide the light from the darkness: and God saw that it was good. And the evening and the morning were the fourth day.
And God said, Let the waters bring forth abundantly the moving creature that hath life, and fowl that may fly above the earth in the open firmament of heaven. And God created great whales, and every living creature that moveth, which the waters brought forth abundantly, after their kind, and every winged fowl after his kind: and God saw that it was good. And God blessed them, saying, Be fruitful, and multiply, and fill the waters in the seas, and let fowl multiply in the earth. And the evening and the morning were the fifth day.
And God said, Let the earth bring forth the living creature after his kind, cattle, and creeping thing, and beast of the earth after his kind: and it was so. And God made the beast of the earth after his kind, and cattle after their kind, and every thing that creepeth upon the earth after his kind: and God saw that it was good. And God said, Let us make man in our image, after our likeness: and let them have dominion over the fish of the sea, and over the fowl of the air, and over the cattle, and over all the earth, and over every creeping thing that creepeth upon the earth. So God created man in his own image, in the image of God created he him; male and female created he them.
And God said, Behold, I have given you every herb bearing seed, which is upon the face of all the earth, and every tree, in the which isthe fruit of a tree yielding seed; to you it shall be for meat. And to every beast of the earth, and to every fowl of the air, and to every thing that creepeth upon the earth, wherein there is life, I have given every green herb for meat: and it was so. And God saw every thing that he had made, and, behold, it was very good. And the evening and the morning were the sixth day.
segunda-feira, 13 de abril de 2015
The first three days of God's Creation in Genesis 01:01-13
In the beginning God created the heaven and the earth. And the earth was without form, and void; and darkness was upon the face of the deep. And the Spirit of God moved upon the face of the waters.
And God said, Let there be light: and there was light. And God saw the light, that it was good: and God divided the light from the darkness. And God called the light Day, and the darkness he called Night. And the evening and the morning were the first day.
And God said, Let there be a firmament in the midst of the waters, and let it divide the waters from the waters. And God made the firmament, and divided the waters which were under the firmament from the waters which were above the firmament: and it was so. And God called the firmament Heaven. And the evening and the morning were the second day.
And God said, Let the waters under the heaven be gathered together unto one place, and let the dry land appear: and it was so. And God called the dry land Earth; and the gathering together of the waters called he Seas: and God saw it was good.
And God said, Let the earth bring forth grass, the herb yielding seed, and the fruit tree yielding fruit after his kind, whose seed is in itself, upon the earth: and it was so. And the earth brought forth grass, and herb yielding seed after his kind, and the tree yielding fruit, whose seed was in itself, after his kind: and God saw that it was good. And the evening and the morning were the third day.
In the beginning God created the heaven and the earth. And the earth was without form, and void; and darkness was upon the face of the deep. And the Spirit of God moved upon the face of the waters.
And God said, Let there be light: and there was light. And God saw the light, that it was good: and God divided the light from the darkness. And God called the light Day, and the darkness he called Night. And the evening and the morning were the first day.
And God said, Let there be a firmament in the midst of the waters, and let it divide the waters from the waters. And God made the firmament, and divided the waters which were under the firmament from the waters which were above the firmament: and it was so. And God called the firmament Heaven. And the evening and the morning were the second day.
And God said, Let the waters under the heaven be gathered together unto one place, and let the dry land appear: and it was so. And God called the dry land Earth; and the gathering together of the waters called he Seas: and God saw it was good.
And God said, Let the earth bring forth grass, the herb yielding seed, and the fruit tree yielding fruit after his kind, whose seed is in itself, upon the earth: and it was so. And the earth brought forth grass, and herb yielding seed after his kind, and the tree yielding fruit, whose seed was in itself, after his kind: and God saw that it was good. And the evening and the morning were the third day.
domingo, 15 de fevereiro de 2015
Number theory
From Wikipedia, the free encyclopedia
Integers can be considered either in themselves or as solutions to equations (Diophantine geometry). Questions in number theory are often best understood through the study of analytical objects (e.g., the Riemann zeta function) that encode properties of the integers, primes or other number-theoretic objects in some fashion (analytic number theory). One may also study real numbers in relation to rational numbers, e.g., as approximated by the latter (Diophantine approximation) .Number theory (or arithmetic) is a branch of pure mathematics devoted primarily to the study of the integers, sometimes called "The Queen of Mathematics" because of its foundational place in the discipline. Number theorists study prime numbers as well as the properties of objects made out of integers (e.g., rational numbers) or defined as generalizations of the integers (e.g., algebraic integers).
The older term for number theory is arithmetic. By the early twentieth century, it had been superseded by "number theory".[note 2] (The word "arithmetic" is used by the general public to mean "elementary calculations"; it has also acquired other meanings in mathematical logic, as in Peano arithmetic, and computer science, as in floating point arithmetic.) The use of the term arithmetic for number theoryregained some ground in the second half of the 20th century, arguably in part due to French influence. In particular, arithmetical is preferred as an adjective to number-theoretic.
Rules of algebra
Rules of algebra
In algebra, there are a few rules that can be used for further understanding of equations. These are called the rules of algebra. While these rules may seem senseless or obvious, it is wise to understand that these properties do not hold throughout all branches of mathematics. Therefore, it will be useful to know how these axiomatic rules are declared, before taking them for granted. Before going on to the rules, reflect on two definitions that will be given.
- Opposite - the opposite of
 is
is 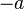 .
. - Reciprocal - the reciprocal of
 is
is  .
.
Rules
Commutative property of addition
'Commutative' means that a function has the same result if the numbers are swapped around. In other words, the order of the terms in an equation do not matter. When the operator of two terms is an addition, the 'commutative property of addition' is applicable. In algebraic terms, this gives 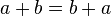 .
.
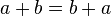 .
.
Note that this does not apply for subtraction! (i.e.  )
)
 )
)Commutative property of multiplication
When the operator of two terms is an multiplication, the 'commutative property of multiplication' is applicable. In algebraic terms, this gives  .
.
 .
.
Note that this does not apply for division! (i.e.  , when
, when  )
)
 , when
, when  )
)Associative property of addition
'Associative' refers to the grouping of numbers. The associative property of addition implies that, when adding three or more terms, it doesn't matter how these terms are grouped. Algebraically, this gives 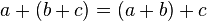 . Note that this does not hold for subtraction, e.g.
. Note that this does not hold for subtraction, e.g.  (see the distributive property).
(see the distributive property).
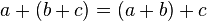 . Note that this does not hold for subtraction, e.g.
. Note that this does not hold for subtraction, e.g.  (see the distributive property).
(see the distributive property).Associative property of multiplication
The associative property of multiplication implies that, when multiplying three or more terms, it doesn't matter how these terms are grouped. Algebraically, this gives  . Note that this does not hold for division, e.g.
. Note that this does not hold for division, e.g.  .
.
 . Note that this does not hold for division, e.g.
. Note that this does not hold for division, e.g.  .
.Distributive property
The distributive property states that the multiplication of a number by another term can be distributed. For instance: 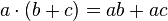 . (Do not confuse this with the associative properties! For instance,
. (Do not confuse this with the associative properties! For instance,  .)
.)
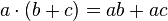 . (Do not confuse this with the associative properties! For instance,
. (Do not confuse this with the associative properties! For instance,  .)
.)Additive identity property
'Identity' refers to the property of a number that it is equal to itself. In other words, there exists an operation of two numbers so that it equals the variable of the sum. The additive identity property states that the sum of any number and 0 is that number:  . This also holds for subtraction:
. This also holds for subtraction: 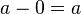 .
.
 . This also holds for subtraction:
. This also holds for subtraction: 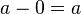 .
.Multiplicative identity property
The multiplicative identity property states that the product of any number and 1 is that number:  . This also holds for division:
. This also holds for division:  .
.
 . This also holds for division:
. This also holds for division:  .
.Additive inverse property
The additive inverse property is somewhat like the opposite of the additive identity property. When an operation is the sum of a number and its opposite, and it equals 0, that operation is a valid algebraic operation. Algebraically, it states the following:  .
.
 .
.Multiplicative inverse property
The multiplicative inverse property entails that when an operation is the product of a number and its reciprocal, and it equals 1, that operation is a valid algebraic operation. Algebraically, it states the following:  .
.
 .
.
By Wikipedia
sexta-feira, 13 de fevereiro de 2015
Algebra and Funcions
An important part of algebra is the study of functions, since functions often appear in equations that we are trying to solve. A function is like a box you can put a number or numbers into and get a certain number out. When using functions, graphs can be powerful tools in helping us to study the solutions to equations.
A graph is a picture that shows all the values of the variables that make the equation or inequality true. Usually this is easy to make when there are only one or two variables. The graph is often a line, and if the line does not bend or go straight up-and-down it can be described by the basic formula y = mx + b. The variable b is the y-intercept of the graph (where the line crosses the vertical axis) and m is theslope or steepness of the line. This formula applies to the coordinates of a graph, where each point on the line is written (x, y).
In some math problems like the equation for a line, there can be more than one variable (x and y in this case). To find points on the line, one variable is changed. The variable that is changed is called the "independent" variable. Then the math is done to make a number. The number that is made is called the "dependent" variable. Most of the time the independent variable is written as x and the dependent variable is written as y, for example, in y = 3x + 1. This is often put on a graph, using an x axis (going left and right) and a y axis (going up and down). It can also be written in function form: f(x) = 3x + 1. So in this example, we could put in 5 for x and get y = 16. Put in 2 for x would get y=7. And 0 for x would get y=1. So there would be a line going thru the points (5,16), (2,7), and (0,1) as seen in the graph to the right.
If x has a power of 1, it is a straight line. If it is squared or some other power, it will be curved. If it uses an inequality (< or >), then usually part of the graph is shaded, either above or below the line.
quinta-feira, 12 de fevereiro de 2015
Algebra II
Algebra II
Early forms of algebra were developed by the Babylonians and the Greeks. However the word "algebra" is a Latin form of the Arabic word Al-Jabr ("casting") and comes from a mathematics book Al-Maqala fi Hisab-al Jabr wa-al-Muqabilah, ("Essay on the Computation of Casting and Equation") written in the 9th century by a famous Persianmathematician, Muhammad ibn Mūsā al-Khwārizmī, who was a Muslim born in Khwarizm in Uzbekistan. He flourished under Al-Ma'moun in Baghdad, Iraq through 813-833 AD, and died around 840 AD. The book was brought into Europe and translated into Latin in the 12th century. The book was then given the name 'Algebra'. (The ending of the mathematician's name, al-Khwarizmi, was changed into a word easier to say in Latin, and became the English word algorithm.)[3]
Examples
Here is a simple example of an algebra problem:
- Sue has 12 jellybeans, Ann has 24 jellybeans. They decide to share so that they have the same number of jellybeans.
These are the steps you can use to solve the problem:
- To have the same number of jellybeans, Ann has to give some to Sue. Let x represent the number of jellybeans Ann gives to Sue.
- Sue's jellybeans, plus x, must be the same as Ann's jellybeans minus x. This is written as: 12 + x = 24 - x
- Subtract 12 from both sides of the equation. This gives: x = 12 - x. (What happens on one side of the equals sign must happen on the other side too, for the equation to still be true. So in this case when 12 was subtracted from both sides, there was a middle step of 12 + x - 12 = 24 - x - 12. After a person is comfortable with this, the middle step is not written down.)
- Add x to both sides of the equation. This gives: 2x = 12
- Divide both sides of the equation by 2. This gives x = 6. The answer is six. If Ann gives Sue 6 jellybeans, they will have the same number of jellybeans.
- To check this, put 6 back into the original equation wherever x was: 12 + 6 = 24 - 6
- This gives 18=18, which is true. They both now have 18 jellybeans.
With practice, algebra can be used when faced with a problem that is too hard to solve any other way. Problems such as building a freeway, designing a cell phone, or finding the cure for a disease all require algebra.
Assinar:
Postagens (Atom)