Rules of algebra
In algebra, there are a few rules that can be used for further understanding of equations. These are called the rules of algebra. While these rules may seem senseless or obvious, it is wise to understand that these properties do not hold throughout all branches of mathematics. Therefore, it will be useful to know how these axiomatic rules are declared, before taking them for granted. Before going on to the rules, reflect on two definitions that will be given.
- Opposite - the opposite of
 is
is 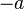 .
. - Reciprocal - the reciprocal of
 is
is  .
.
Rules
Commutative property of addition
'Commutative' means that a function has the same result if the numbers are swapped around. In other words, the order of the terms in an equation do not matter. When the operator of two terms is an addition, the 'commutative property of addition' is applicable. In algebraic terms, this gives 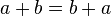 .
.
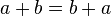 .
.
Note that this does not apply for subtraction! (i.e.  )
)
 )
)Commutative property of multiplication
When the operator of two terms is an multiplication, the 'commutative property of multiplication' is applicable. In algebraic terms, this gives  .
.
 .
.
Note that this does not apply for division! (i.e.  , when
, when  )
)
 , when
, when  )
)Associative property of addition
'Associative' refers to the grouping of numbers. The associative property of addition implies that, when adding three or more terms, it doesn't matter how these terms are grouped. Algebraically, this gives 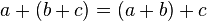 . Note that this does not hold for subtraction, e.g.
. Note that this does not hold for subtraction, e.g.  (see the distributive property).
(see the distributive property).
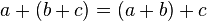 . Note that this does not hold for subtraction, e.g.
. Note that this does not hold for subtraction, e.g.  (see the distributive property).
(see the distributive property).Associative property of multiplication
The associative property of multiplication implies that, when multiplying three or more terms, it doesn't matter how these terms are grouped. Algebraically, this gives  . Note that this does not hold for division, e.g.
. Note that this does not hold for division, e.g.  .
.
 . Note that this does not hold for division, e.g.
. Note that this does not hold for division, e.g.  .
.Distributive property
The distributive property states that the multiplication of a number by another term can be distributed. For instance: 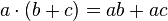 . (Do not confuse this with the associative properties! For instance,
. (Do not confuse this with the associative properties! For instance,  .)
.)
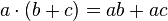 . (Do not confuse this with the associative properties! For instance,
. (Do not confuse this with the associative properties! For instance,  .)
.)Additive identity property
'Identity' refers to the property of a number that it is equal to itself. In other words, there exists an operation of two numbers so that it equals the variable of the sum. The additive identity property states that the sum of any number and 0 is that number:  . This also holds for subtraction:
. This also holds for subtraction: 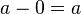 .
.
 . This also holds for subtraction:
. This also holds for subtraction: 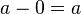 .
.Multiplicative identity property
The multiplicative identity property states that the product of any number and 1 is that number:  . This also holds for division:
. This also holds for division:  .
.
 . This also holds for division:
. This also holds for division:  .
.Additive inverse property
The additive inverse property is somewhat like the opposite of the additive identity property. When an operation is the sum of a number and its opposite, and it equals 0, that operation is a valid algebraic operation. Algebraically, it states the following:  .
.
 .
.Multiplicative inverse property
The multiplicative inverse property entails that when an operation is the product of a number and its reciprocal, and it equals 1, that operation is a valid algebraic operation. Algebraically, it states the following:  .
.
 .
.
By Wikipedia
Nenhum comentário:
Postar um comentário